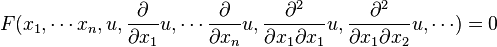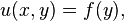La derivada es uno de los conceptos más importante en matemáticas. La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto. Pero vayamos por partes.
LO MEJOR DE LA DERIVACION
domingo, 29 de mayo de 2011
la derivada se representa cómo una función que cambia (valor de la variable dependiente) a medida que su entrada (valor de la variable independiente) cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una función en un punto dado (o sea su velocidad de variación); por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo, es la velocidad instantánea con la cual el vehículo está viajando.
REGLAS DE LA DERIVACION
Derivada de una suma Se puede demostrar a partir de la definición de derivada, que la derivada de la suma de dos funciones es la suma de las derivadas de cada una. Es decir, (f + g)' = f' + g'. Como ejemplo consideremos la función f(x) = 3x5 + x3, para determinar su derivada se trabaja la derivada de cada término aparte y la suma de ambos será la derivada de la función:
f'(x) = 15x4 + 3x2
Derivada de un producto
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de dos funciones es equivalente a la suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función"
Y matemáticamente expresado por la relación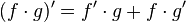 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo:
h(x) = (4x + 2)(3x7 + 2)
Identificamos a f(x) = (4x + 2) y g(x) = (3x7 + 2), utilizando las reglas anteriormente expuestas, vemos que:
f'(x) = 4 y que g'(x) = 21x6
Por lo tanto
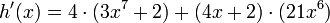
Simplificando y organizando el producto obtenido nos queda
h'(x) = 84x7 + 12x7 + 42x6 + 8
Sumamos términos semejantes y finalmente obtenemos la derivada:
h'(x) = 96x7 + 42x6 + 8
Si por ejemplo tenemos la derivada del producto de tres funciones que dependen de la misma variable, podemos pensar el producto de dos de las funciones como si se tratara de una tercera función es decir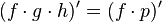 en donde
en donde 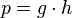 (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).
Derivada de un cociente
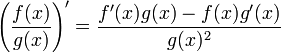
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:
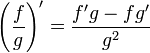
Es decir:
"La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado".
Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es g(x) = 2x y se multiplique por la derivada del numerador que seria f'(x) = 3; luego la segunda parte dice que tomemos la función del numerador (f(x)) sin derivar y lo multipliquemos por la derivada de g(x) = 2x, que seria g'(x) = 2, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar:
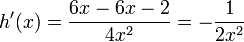
f'(x) = 15x4 + 3x2
Derivada de un producto
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de dos funciones es equivalente a la suma entre el producto de la primera función sin derivar y la derivada de la segunda función y el producto de la derivada de la primera función por la segunda función"
Y matemáticamente expresado por la relación
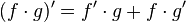 . Consideremos la siguiente función como ejemplo:
. Consideremos la siguiente función como ejemplo:h(x) = (4x + 2)(3x7 + 2)
Identificamos a f(x) = (4x + 2) y g(x) = (3x7 + 2), utilizando las reglas anteriormente expuestas, vemos que:
f'(x) = 4 y que g'(x) = 21x6
Por lo tanto
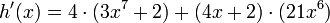
Simplificando y organizando el producto obtenido nos queda
h'(x) = 84x7 + 12x7 + 42x6 + 8
Sumamos términos semejantes y finalmente obtenemos la derivada:
h'(x) = 96x7 + 42x6 + 8
Si por ejemplo tenemos la derivada del producto de tres funciones que dependen de la misma variable, podemos pensar el producto de dos de las funciones como si se tratara de una tercera función es decir
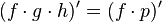 en donde
en donde 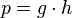 (sin importar que dos funciones escogemos).
(sin importar que dos funciones escogemos).Derivada de un cociente
La derivada de un cociente se determina por la siguiente relación:
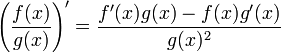
Para aquellos que se puedan confundir por algunas variables de más se puede escribir así:
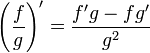
Es decir:
"La derivada de un cociente de dos funciones es la función ubicada en el denominador por la derivada del numerador menos la derivada de la función en el denominador por la función del numerador sin derivar, todo sobre la función del denominador al cuadrado".
Este caso se relaciona mucho con la regla de derivada de un producto, pero hay que tener en cuenta la resta y el orden de los factores. Pero ya explicando lo dicho anteriormente consideremos como ejemplo la siguiente función:

Ahora se trabaja el enunciado anterior el cual nos dice que multipliquemos el denominador que en este caso es g(x) = 2x y se multiplique por la derivada del numerador que seria f'(x) = 3; luego la segunda parte dice que tomemos la función del numerador (f(x)) sin derivar y lo multipliquemos por la derivada de g(x) = 2x, que seria g'(x) = 2, todo esto lo dividimos entre el denominador al cuadrado, así:

Ahora todo es cuestión de simplificar:
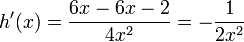
HISTORIA
 Los problemas típicos que dieron origen al Cálculo Infinitesimal, comenzaron a plantearse en la época clásica de Grecia (siglo III a.C.), pero, no se encontraron métodos sistemáticos de resolución hasta 20 siglos después (en el siglo XVII por obra de Newton y Leibnitz).
Los problemas típicos que dieron origen al Cálculo Infinitesimal, comenzaron a plantearse en la época clásica de Grecia (siglo III a.C.), pero, no se encontraron métodos sistemáticos de resolución hasta 20 siglos después (en el siglo XVII por obra de Newton y Leibnitz). En lo que atañe a las derivadas, existen dos conceptos de tipo geométrico: el problema de la tangente a una curva (concepto griego estático en contraste con el concepto cinemático de Arquímedes) y el problema de los extremos (máximos y mínimos) que en su conjunto dieron origen a lo que modernamente se conoce como Cálculo Diferencial.
El problema de la tangente a una curva, fue analizado y resuelto primeramente por Apolonio (200 a.C.). En el libro II de su obra, hace el estudio de los diámetros conjugados y de las tangentes a una cónica. Por ejemplo, si P es un punto cualquiera de una hipérbola de centro C, entonces, Apolonio demuestra que la tangente en P corta las asíntotas en los puntos L y L’ (fig. 9.1. (a)) que equidistan de P.
 |  |
(a) (b)
En el caso de la elipse, si Q es un punto de la curva (fig. 9.1. (b)), Apolonio traza la perpendicular  desde el punto Q al eje AA’, y halla el conjugado armónico T de N con respecto a A y A’, es decir, el punto T de la recta AA’ es tal que
desde el punto Q al eje AA’, y halla el conjugado armónico T de N con respecto a A y A’, es decir, el punto T de la recta AA’ es tal que  , o equivalentemente, el punto T que divide externamente al segmento AA’ en la misma razón en que N divide internamente a AA’. Entonces, la recta que pasa por T y Q será tangente a la elipse.
, o equivalentemente, el punto T que divide externamente al segmento AA’ en la misma razón en que N divide internamente a AA’. Entonces, la recta que pasa por T y Q será tangente a la elipse.
Igualmente, en el libro CÓNICAS V.8., Apolonio demuestra un teorema relativo a la normal a una parábola, que podría formar parte actualmente de un curso completo de Cálculo Diferencial.
En cuanto al problema de los extremos relativos de una función, fue Pierre de Fermat (1601 – 1665) quien en el año 1629, hizo dos importantes descubrimientos que están relacionados con sus trabajos sobre lugares geométricos. En el mas importante de ellos, titulado Methodus ad disquirendam maximan et miniman ("Métodos para hallar máximos y mínimos"), Fermat expone un método muy ingenioso para hallar los puntos en los cuales una función polinómica de la forma y = f (x), toma un valor máximo o mínimo. Fermat comparaba el valor de f (x) en un cierto punto, con el valor de f (x + E) en un punto próximo; en general, estos dos valores son distintos, pero, en una "cumbre" o en el fondo de un "valle" de una curva "lisa" la diferencia es casi imperceptible. Por lo tanto, para hallar los puntos que corresponden a valores máximos o mínimos de una función, Fermat iguala f (x) con f (x + E), teniendo en cuenta que estos valores son "casi iguales". Cuanto mas pequeña sea la diferencia E entre los dos puntos, mas cerca está la igualdad de ser verdadera. Así, después de dividir todo por E, hace E = 0. El resultado le permite calcular las abscisas de los máximos y mínimos de la función polinómica. Aquí se puede ver ya en esencia, el proceso que ahora se llama diferenciación, ya que el método de Fermat es equivalente a calcular:
. 

Esta fue la razón que asistió a Laplace al aclamar a Fermat como el verdadero descubridor del Cálculo Diferencial. Sin embargo, aunque son muchos y numerosos los precursores, algunos historiadores han considerado que es a Newton (sir Isaac Newton. 1642 – 1727. Nacido en Woolstharpe (Inglaterra)) y a Leibnitz (Gottgried Wilhelm Leibnitz. 1646 – 1716. Nacido en Leipzig (Alemania)) a quienes se les puede atribuir justificadamente la invención de las derivadas y de las integrales.
Newton, tardó mucho en dar a conocer sus resultados. La notación que usaba era mas sugestiva: lo que nosotros llamamos f (x) ó y, él lo llamaba "cantidades fluentes", y la derivada, D f (x) era llamaba "fluxión". Además, se le escribía  en lugar de D f (x). El mismo Newton escribía cosas como las siguientes: "Los momentos - las actuales diferenciales - dejan de ser momentos cuando alcanzan un valor finito, y deben por lo tanto considerarse como magnitudes finitas nacientes". Frases tan confusas, que Newton debía entenderlas muy bien, pero, para otro que no fuera su inventor del método, suenan bastante incomprensibles.
en lugar de D f (x). El mismo Newton escribía cosas como las siguientes: "Los momentos - las actuales diferenciales - dejan de ser momentos cuando alcanzan un valor finito, y deben por lo tanto considerarse como magnitudes finitas nacientes". Frases tan confusas, que Newton debía entenderlas muy bien, pero, para otro que no fuera su inventor del método, suenan bastante incomprensibles.
ecuacines de derivacion:
Una ecuación en derivadas parciales (EDP) para la función u(x1,...xn) tiene la siguiente forma

Si F es una función lineal de u y sus derivadas, entonces la EDP es lineal. Ejemplos comunes de EDPs son la ecuacion de calor, la ecuacion de honda
Una ecuación en derivadas parciales muy simple puede ser:
donde f es una función arbitraria de y. La ecuacion diferncial ordinaria (Similar a la EDP, pero con funciones de una variable) análoga es
que tiene la siguiente solución
Donde c es cualquier valor constante (independiente de x). Estos dos ejemplos ilustran que las soluciones generales de las ecuaciones diferenciales ordinarias se mantienen con constantes, pero las soluciones de las ecuaciones diferenciales en derivadas parciales generan funciones arbitrarias. Una solución de una ecuación en derivadas parciales generalmente no es unica; de esta forma se tienen que proporcionar condiciones adicionales de contorno capaces de definir la solución de forma única. Por ejemplo, en el caso sencillo anterior, la función f(y) puede determinarse si u se especifica sobre la línea x = 0
Función derivada
La función derivada de una función f(x) es una función que asocia a cada número real su derivada, si existe. Se denota por f'(x).
Derivadas laterales
Derivada por la izquierda
Derivada por la derecha

Suscribirse a:
Entradas (Atom)